| Trees | Indices | Help |
|
|---|
|
|

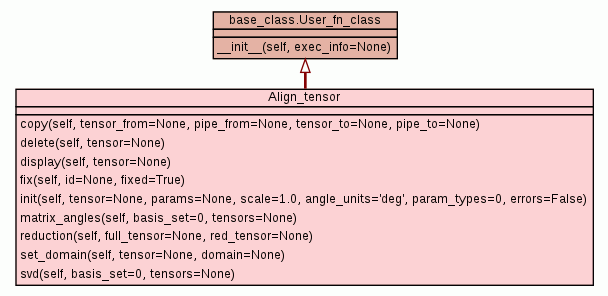
Class for manipulating the alignment tensor.
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
|||
|
Inherited from |
|||
|
|||
Function for copying alignment tensor data.
Keyword Arguments
~~~~~~~~~~~~~~~~~
tensor_from: The identification string of the alignment tensor to copy the data from.
pipe_from: The name of the data pipe to copy the alignment tensor data from.
tensor_to: The identification string of the alignment tensor to copy the data to.
pipe_to: The name of the data pipe to copy the alignment tensor data to.
Description
~~~~~~~~~~~
This function will copy the alignment tensor data to a new tensor or a new data pipe. The
destination data pipe must not contain any alignment tensor data corresponding to the
tensor_to label. If the pipe_from or pipe_to arguments are not supplied, then both will
default to the current data pipe. Both the tensor_from and tensor_to arguments must be
supplied.
Examples
~~~~~~~~
To copy the alignment tensor data corresponding to 'Pf1' from the data pipe 'old' to the
current data pipe, type one of:
relax> align_tensor.copy('Pf1', 'old')
relax> align_tensor.copy(tensor_from='Pf1', pipe_from='old')
To copy the alignment tensor data corresponding to 'Otting' from the current data pipe to
the data pipe new, type one of:
relax> align_tensor.copy('Otting', pipe_to='new')
relax> align_tensor.copy(tensor_from='Otting', pipe_to='new')
To copy the alignment tensor data of 'Otting' to that of 'Otting new', type one of:
relax> align_tensor.copy('Otting', tensor_to='Otting new')
relax> align_tensor.copy(tensor_from='Pf1', tensor_to='Otting new')
|
Function for deleting alignment tensor data. Keyword Arguments ~~~~~~~~~~~~~~~~~ tensor: The alignment tensor identification string. Description ~~~~~~~~~~~ This function will delete the specified alignment tensor data from the current data pipe. |
Function for displaying the alignment tensor information. Keyword Arguments ~~~~~~~~~~~~~~~~~ tensor: The alignment tensor identification string. |
Fix all alignment tensors so that they do not change during optimisation. Keyword Arguments ~~~~~~~~~~~~~~~~~ id: The alignment tensor identification string. fixed: The flag specifying if the tensors should be fixed or variable. Description ~~~~~~~~~~~ If the ID string is left unset, then all alignment tensors will be fixed. |
Function for initialising the alignment tensor.
Keyword Arguments
~~~~~~~~~~~~~~~~~
tensor: The alignment tensor identification string.
params: The alignment tensor data.
scale: The alignment tensor eigenvalue scaling value.
angle_units: The units for the angle parameters.
param_types: A flag to select different parameter combinations.
errors: A flag which determines if the alignment tensor data or its errors are being input.
Description
~~~~~~~~~~~
Using this function, the alignment tensor data can be set up. The params argument should be
a tuple of floating point numbers (a list surrounded by round brakets). These correspond to
the parameters of the tensor, which can be specified by the param_types argument, where the
values correspond to
0: {Sxx, Syy, Sxy, Sxz, Syz} (unitless),
1: {Szz, Sxx-yy, Sxy, Sxz, Syz} (Pales default format),
2: {Axx, Ayy, Axy, Axz, Ayz} (unitless),
3: {Azz, Axx-yy, Axy, Axz, Ayz} (unitless),
4: {Axx, Ayy, Axy, Axz, Ayz} (units of Hertz),
5: {Azz, Axx-yy, Axy, Axz, Ayz} (units of Hertz),
6: {Pxx, Pyy, Pxy, Pxz, Pyz} (unitless),
7: {Pzz, Pxx-yy, Pxy, Pxz, Pyz} (unitless),
Other formats may be added later. The relationship between the Saupe order matrix S and the
alignment tensor A is
S = 3/2 A.
The probability matrix P is related to the alignment tensor A by
A = P - 1/3 I,
where I is the identity matrix. For the alignment tensor to be supplied in Hertz, the bond
vectors must all be of equal length.
Examples
~~~~~~~~
To set a rhombic tensor to the run 'CaM', type one of:
relax> align_tensor.init('super media', (-8.6322e-05, -5.5786e-04, -3.1732e-05, 2.2927e-05,
2.8599e-04), param_types=1)
relax> align_tensor.init(tensor='super media', params=(-8.6322e-05, -5.5786e-04,
-3.1732e-05, 2.2927e-05, 2.8599e-04), param_types=1)
|
Function for calculating the 5D angles between all alignment tensors.
Keyword Arguments
~~~~~~~~~~~~~~~~~
basis_set: The basis set to operate with.
tensors: A list of the tensors to apply the calculation to. If None, all tensors are used.
Description
~~~~~~~~~~~
This function will calculate the angles between all loaded alignment tensors for the current
data pipe. The matrices are first converted to a 5D vector form and then then angles are
calculated. The angles are dependent on the basis set. If the basis_set argument is set to
the default of 0, the vectors {Sxx, Syy, Sxy, Sxz, Syz} are used. If the basis_set argument
is set to 1, the vectors {Szz, Sxxyy, Sxy, Sxz, Syz} are used instead.
|
Specify that one tensor is a reduction of another. Keyword Arguments ~~~~~~~~~~~~~~~~~ full_tensor: The full alignment tensor. red_tensor: The reduce alignment tensor. Description ~~~~~~~~~~~ Prior to optimisation of the N-state model and Frame Order theories using alignment tensors, which tensor is a reduction of which other tensor must be specified through this user function. Examples ~~~~~~~~ To state that the alignment tensor loaded as 'chi3 C-dom' is a reduction of 'chi3 N-dom', type: relax> align_tensor.reduction(full_tensor='chi3 N-dom', red_tensor='chi3 C-dom') |
Set the domain label for the alignment tensor. Keyword Arguments ~~~~~~~~~~~~~~~~~ tensor: The alignment tensor to assign the domain label to. domain: The domain label. Description ~~~~~~~~~~~ Prior to optimisation of the N-state model or Frame Order theories, the domain to which each alignment tensor belongs must be specified. Examples ~~~~~~~~ To link the alignment tensor loaded as 'chi3 C-dom' to the C-terminal domain 'C', type: relax> align_tensor.set_domain(tensor='chi3 C-dom', domain='C') |
Function for calculating the singular values for all tensors and the condition number.
Keyword Arguments
~~~~~~~~~~~~~~~~~
basis_set: The basis set to operate with.
tensors: A list of the tensors to apply the calculation to. If None, all tensors are used.
Description
~~~~~~~~~~~
This function will, using SVD, calculate the singular values of all tensors loaded for the
current data pipe. If the basis_set argument is set to the default of 0, the matrix on
which SVD will be performed is composed of the unitary basis set {Sxx, Syy, Sxy, Sxz, Syz}
layed out as:
-----
| Sxx1 Syy1 Sxy1 Sxz1 Syz1 |
| Sxx2 Syy2 Sxy2 Sxz2 Syz2 |
| Sxx3 Syy3 Sxy3 Sxz3 Syz3 |
| . . . . . |
| . . . . . |
| . . . . . |
| SxxN SyyN SxyN SxzN SyzN |
-----
If basis_set is set to 1, the geometric basis set consisting of the stretching and skewing
parameters Szz and Sxx-yy respectively {Szz, Sxxyy, Sxy, Sxz, Syz} will be used instead.
The matrix is:
-----
| Szz1 Sxxyy1 Sxy1 Sxz1 Syz1 |
| Szz2 Sxxyy2 Sxy2 Sxz2 Syz2 |
| Szz3 Sxxyy3 Sxy3 Sxz3 Syz3 |
| . . . . . |
| . . . . . |
| . . . . . |
| SzzN SxxyyN SxyN SxzN SyzN |
-----
The relationships between the geometric and unitary basis sets are:
-----
Szz = - Sxx - Syy,
Sxxyy = Sxx - Syy,
-----
The SVD values and condition number are dependendent upon the basis set chosen.
|
| Trees | Indices | Help |
|
|---|
| Generated by Epydoc 3.0.1 on Wed Apr 10 13:31:50 2013 | http://epydoc.sourceforge.net |