relax: dynamics analysis, model-free analysis, relaxation data, R1 and R2 exponential curve-fitting, steady-state NOE calculation, reduced spectral density mapping, relaxation dispersion, N-state model, frame order dynamics theories, stereochemistry, conformational analysis, organic molecules, proteins, RNA, DNA, sugars, and other biomolecules.
relax: dynamics analysis, model-free analysis, relaxation data, R1 and R2 exponential curve-fitting, steady-state NOE calculation, reduced spectral density mapping, relaxation dispersion, N-state model, frame order dynamics theories, stereochemistry, conformational analysis, organic molecules, proteins, RNA, DNA, sugars, and other biomolecules.

relax - Molecular dynamics by NMR data analysis

Analysis software for: Model-free, NMR relaxation (R1, R2, NOE), reduced spectral density mapping, relaxation dispersion, N-state models, frame order theory.

The relax menu
relax: dynamics analysis, model-free analysis, relaxation data, R1 and R2 exponential curve-fitting, steady-state NOE calculation, reduced spectral density mapping, relaxation dispersion, N-state model, frame order dynamics theories, stereochemistry, conformational analysis, organic molecules, proteins, RNA, DNA, sugars, and other biomolecules.

Relaxation dispersion analysis

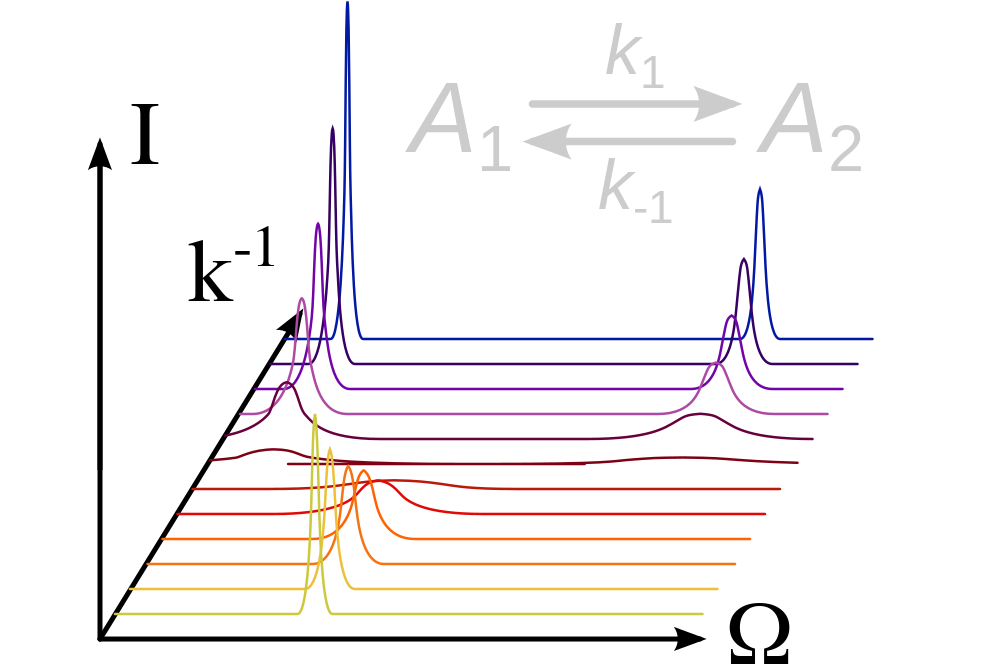
Relaxation dispersion in NMR: The magnetic field strength dependence of chemical shifts

The software relax supports the analysis of NMR relaxation dispersion data (see Morin et al., 2014). All dispersion data types are supported as well as an almost complete list of relaxation dispersion models, both analytic and numeric.

Data types

The following relaxation dispersion data types are supported by relax:

Models

Numerous analytic and numeric relaxation dispersion models are supported by relax. It the model you are interested is not yet supported, please see the tutorial for adding dispersion models to relax.

Experiment independent models

The following models are independent of the experiment type:

Analytic models for SQ CPMG-type experiments

The following analytic models are designed for the standard single quantum CPMG-type experiments:

  • 'LM63': The original Luz and Meiboom 1963 2-site fast exchange equation with parameters {R20, ..., Φex, kex}. (See the wiki, manual, API documentation).
  • 'LM63 3-site': The original Luz and Meiboom 1963 3-site fast exchange equation with parameters {R20, ..., ΦexB, kB, ΦexC, kC}. (See the wiki, manual, API documentation).
  • 'CR72': The reduced Carver and Richards 1972 2-site equation for most time scales whereby the simplification R2A0 = R2B0 is assumed. It has the parameters {R20, ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'CR72 full': The full Carver and Richards 1972 2-site equation for most time scales with the parameters {R2A0, R2B0, ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'IT99': The Ishima and Torchia 1999 2-site model for all time scales with pA » pB and with parameters {R20, ..., pA, Δω, tex}. (See the wiki, manual, API documentation).
  • 'TSMFK01': The Tollinger et al., 2001 2-site very-slow exchange model for time scales within range of microsecond to second time scale. Applicable in the limit of slow exchange, when R2A0 - R2B0 « kAB, kBA « 1/τCPMG. 2*τCPMG is the time between successive 180 degree pulses. The parameters are {R2A0, ..., Δω, kAB}. (See the wiki, manual, API documentation).
  • 'B14': The reduced Baldwin 2014 2-site equation for all time scales whereby the simplification R2A0 = R2B0 is assumed. It has the parameters {R20, ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'B14 full': The full Baldwin 2014 2-site equation for all time scales with the parameters {R2A0, R2B0, ..., pA, Δω, kex}. (See the wiki, manual, API documentation).

Numeric models for SQ CPMG-type experiments

The following analytic models are designed for the standard single quantum CPMG-type experiments:

Analytic models for MMQ-type data

The following analytic models are designed for combined proton-heteronuclear SQ, ZQ, DQ and MQ (MMQ, or multiple MQ) CPMG-type experiments:

  • 'MMQ CR72': The Carver and Richards (1972) 2-site model for most time scales expanded for MMQ CPMG data by Korzhnev et al., 2004. It has the parameters {R20, ..., pA, Δω, ΔωH, kex}. (See the wiki, manual, API documentation).

Numeric models for MMQ-type data

The following numeric models are designed for MMQ CPMG-type experiments:

  • 'NS MMQ 2-site': The model for 2-site exchange whereby the simplification R2A0 = R2B0 is assumed. It has the parameters {R20, ..., pA, Δω, ΔωH, kex}. (See the wiki, manual, API documentation).
  • 'NS MMQ 3-site linear': The model for 3-site exchange linearised with kAC = kCA = 0 whereby the simplification R2A0 = R2B0 = R2C0 is assumed. It has the parameters {R20, ..., pA, ΔωAB, ΔωBC, ΔωABH, ΔωBCH, kexAB, kexBC, kexAC}. (See the wiki, manual, API documentation).
  • 'NS MMQ 3-site': The model for 3-site exchange whereby the simplification R2A0 = R2B0 = R2C0 is assumed. It has the parameters {R20, ..., pA, ΔωAB, ΔωBC, ΔωABH, ΔωBCH, kexAB, kexBC, kexAC}. (See the wiki, manual, API documentation).

Analytic models for R1rho experiments

The following analytic models are designed for R1ρ-type experiments:

  • 'M61': The Meiboom 1961 2-site fast exchange equation for on-resonance data with parameters {R1ρ', ..., Φex, kex}. (See the wiki, manual, API documentation).
  • 'M61 skew': The Meiboom 1961 2-site equation for all time scales with pA » pB and with parameters {R1ρ', ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'DPL94': The Davis et al., 1994 extension of the M61 model for off-resonance data with parameters {R1ρ', ..., Φex, kex}. (See the wiki, manual, API documentation).
  • 'TP02': The Trott and Palmer 2002 2-site equation for all time scales with pA » pB and with parameters {R1ρ', ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'TAP03': The Trott et al., 2003 off-resonance 2-site analytic equation for all time scales with the weak condition pA » pB and with parameters {R1ρ', ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'MP05': The Miloushev and Palmer 2005 off-resonance 2-site equation for all time scales with parameters {R1ρ', ..., pA, Δω, kex}. (See the wiki, manual, API documentation).

Numeric models for R1rho experiments

The following numeric models are designed for R1ρ-type experiments:

  • 'NS R1rho 2-site': The model for 2-site exchange using 3D magnetisation vectors. It has the parameters {R1ρ', ..., pA, Δω, kex}. (See the wiki, manual, API documentation).
  • 'NS R1rho 3-site linear': The model for 3-site exchange linearised with kAC = kCA = 0 whereby the simplification R1ρA' = R1ρB' = R1ρC' is assumed. It has the parameters {R1ρ', ..., pA, pB, ΔωAB, ΔωBC, kexAB, kexBC}. (See the wiki, manual, API documentation).
  • 'NS R1rho 3-site': The model for 3-site exchange whereby the simplification R1ρA' = R1ρB' = R1ρC' is assumed. It has the parameters {R1ρ', ..., pA, pB, ΔωAB, ΔωBC, kexAB, kexBC, kexAC}. (See the wiki, manual, API documentation).
This text is available under the terms of the GNU Free Documentation License, Version 1.3 or any later version published by the Free Software Foundation.